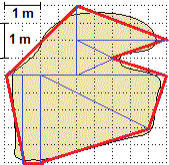
Abbiamo visto che l'area di un terreno o di una figura piana può essere calcolata approssimandone il contorno con un poligono e calcolando l'area di questo spezzandolo in triangoli, rettangoli o trapezi di cui so calcolare le aree e, poi, sommando queste. In modo analogo posso calcolare, ad esempio, l'area tra il grafico della funzione  x → 1 − x²  e l'asse x. Sotto i valori che ottengo approssimando il grafico con 2 segmenti, con 3 segmenti, con 4 segmenti, con 5 segmenti, … con qualche migliaia di segmenti:

 Posso sicuramente concludere che quest'area vale 1+1/3 = 4/3.

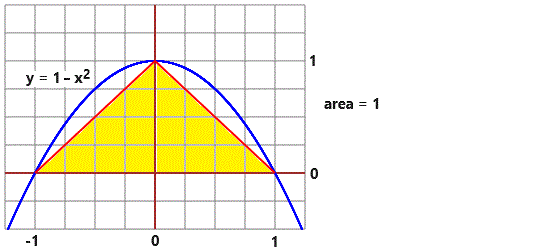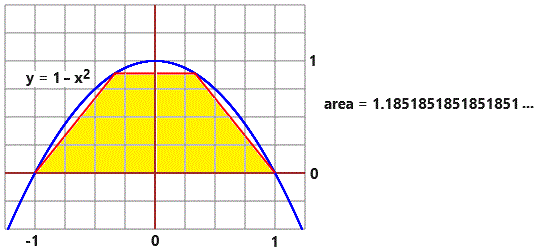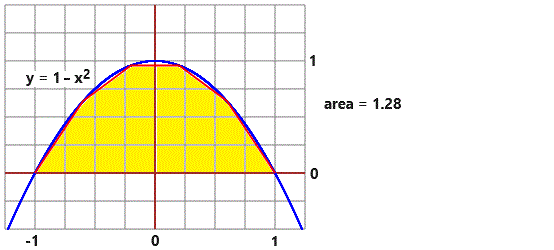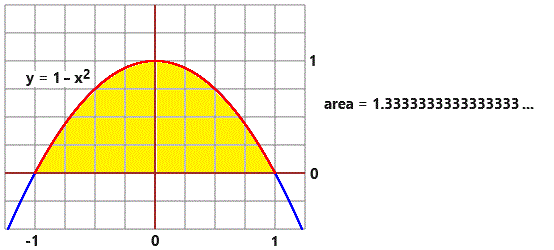
Potevo approssimare l'area anche con un istogramma formato da un numero crescente di rettangolini.  Ecco a lato che cosa si ottiene per un semicerchio di raggio 1, approssimato con 4, 8, 16, 32, 64 rettangolini:  una successione di valori che tende a π/2 = 1.570796… in accordo con quanto già sappiamo: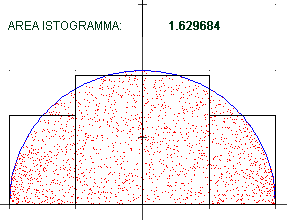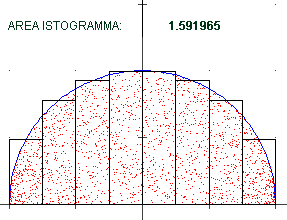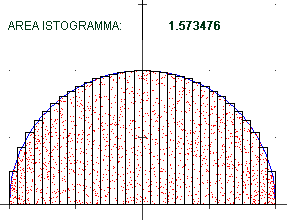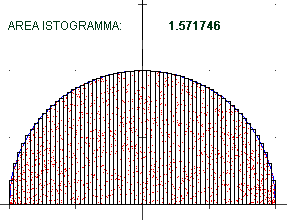

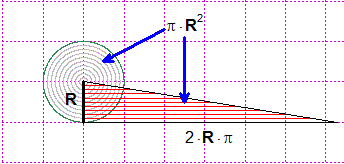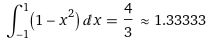Vediamo come si può fare il calcolo considerato all'inizio con WolframAlpha: 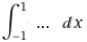area between y = 1-x^2, y = 0 in accordo con quanto abbiamo già visto.  Sul significato del simbolo               (che si legge "integrale tra -1 ed 1 di ...") ti soffermerai fra poco nel corso degli studi.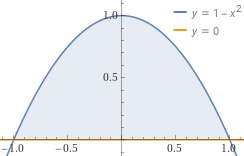